After we have been qualified at the online filtration phase. We
attended
Arab Security Wargames
on-site on 12th of Sep and my team
Revers3c
got the 1st place (The Titan). Actually, the
challenges were so awesome and we had a lot of fun with them. As
in my little knowledge in Cryptography and
loving the math behind it, there was 6 cool crypto challenges
among all 5 categories, and I’ll go through explaining each one
of them.
Table of Content:
- Hashes (300 points)
- Retrieve (300 points)
- Hybrid (600 points)
- Robin Hood (600 points)
- Simple RSA (900 points)
- RSA in Hill (900 points)
1. Hashes (300 points)
This was the first and also simple challenge, we were given an
encryption script
encrypt.py
and
cipher.txt
that contains the
base64
of the
data.
So let’s look at the script to see what it does.
import hashlib
flag = open("flag.txt").read().replace("\n","")
cipher = open("cipher.txt","w")
hash = ""
for char in flag:
hash+=hashlib.sha512(hashlib.md5(hashlib.sha512(char).hexdigest()).hexdigest()).hexdigest()
hash = hash[::-1].encode("base64")
cipher.write(hash)
The script reads the flag, iterates over it charachter by
charachter, then performs
sha512(md5(sha512(char)))
on each one, and finally encodes the result with
base64
after reversing it.
Solution
Hopefully, this is a well-known attack called
message signing, so we can encrypt a specific
value and check if it is equal to the encrypted one. If so then
this value is what we want otherwise, try another one. We can
see the length of each character hashing is
128,
so I wrote a script to try every possible character and print
the flag.
#!/usr/bin/env python3
import base64
import hashlib
import string
LEN = 128
flag = ''
with open('cipher.txt', 'rb') as h:
hash = base64.b64decode(h.read()).decode()[::-1]
def H(c):
return hashlib.sha512(hashlib.md5(hashlib.sha512(c).hexdigest().encode()).hexdigest().encode()).hexdigest()
for i in range(0,len(hash),LEN):
for c in string.printable:
if H(c.encode()) == hash[i:i+LEN]:
flag += c
break
print(flag)
The flag:
ACSWG{Brute_F@RCE_1S_G00D_1337_7331_3317_3137_}
2. Retrive (300 points)
Alice intercepted a part of a plaintext but a there’s a small part he could not intercept . can u help alice ? Intercepted part : ASCWG{y0u_N33d_t0Brut3_F0rce_th3
This one is a pretty straightforward, given
retrive.py
and
c.txt
that contains
n, e, c. And the script wants us to brute force the last few bytes of
the flag.
from Crypto.Util.number import getPrime
from gmpy import invert
def generate_key():
p = getPrime(2048)
q = getPrime(2048)
n = p*q
phi = (p-1) * (q-1)
e = 65537
d = invert(e,phi)
return [n,e,d]
m = "ASCWG{y0u_N33d_t0_Brut3_F0rce_th3_???"
m = int(m.encode("hex"),16)
n,e,d = generate_key()
c = pow(m,e,n)
print "n = " , n
print "e = " ,e
print "c =",cSolution
Also, this is the same attack as the above but with a bigger value. At first, I thought if the last bytes more than 6 characters then the search space is not feasible since we’ll try all the possible values of the last part. So later on, I realized that it’s an easy one so let’s start with 3 bytes and the last one is known.
#!/usr/bin/env python3
from string import printable, ascii_lowercase, digits
from itertools import product
from Crypto.Util.number import bytes_to_long
n = 876566193838643237337037920433795395573374494439847624125385186386835670267615151865098745626775955776093005136573336594225795853288612401732675263511044369610643107788969933380308966296368853370342299577287721981114487406530956439312605695190916394624794947543008200996555824410091666127523908085602231209361792478776410877076888333247731536986964520985826391032724092756503520728675425243410598251490041662376499017516031354615443801594990171009789066223085666376506651130694586816909765257490655359598764448201972907006552712592359832076831449528162845622085187680039752386917638159778358501612689078221288768506095617646584977689778168775244944940754640428162121779159713615864545373630589517739480041685204898020498897150024659849650137706680607429904678286830423552034212968345168786930394033886118487755695408749531035093665089023658776744679123489557498803084931515122125872209565805780974038555647525297280449197815947206811507039476379978178227948956939287471769147030714588752817587402141286308265488394250857135469355999116760185590145541923393956102918954578026603681023546352683233943437403177607371005525105556052647623797414693596959480739968475803643210012082334972585491836570866138920752937790968378241237334539741
e = 65537
c = 50423365462223754926258130508333729507591338946389232993927416356397813609630082901065628999339238485797666399820826108019185899034418587932574100242741171545584155935738684194850397205415114141757555652038117842779989453467312001210216882334829972216065340743680393415862438814524581080670083590548348048857760554550737040684503631821931495383119153231294458992365341096770173216880436925891892303409282118998437238511507799330980860970580283865238958688730050628166452225308220296582574916401284227618808886352604625809424257929880999115121852970111670130157251706541043336875497776236002536707914909824427907853005098805568813345743125421221126029219358222153652926946515854823586278913614872736714077040426294670803571765863871770541158097065630542563760859963818818564306964335900936804624971263060469051147522366500260917487649295038676727824471401365516551898207907163352878181099533324423266298541882681454099876005303861352749938624642162065114121305377632631163771373596450657300893012099392095762449126286406969595033889245616377701666788882986799484780786853142699953327087663804243726310393803765185300094349658941306879523687762914924166069216225493181485871584266122421952690581199085496269689191977348149262399232601
flag = 'ASCWG{y0u_N33d_t0_Brut3_F0rce_th3_???}'
letters = ascii_lowercase + digits
for p in product(letters, letters, letters):
val = bytes_to_long(flag.replace('???', ''.join(p)).encode())
if pow(val,e,n) == c:
print(flag.replace('???', ''.join(p)))
break
And it prints the flag:
ASCWG{y0u_N33d_t0_Brut3_F0rce_th3_k3y}
3. Hybrid (600 points)
This challenge is a bit tricky, also with
2
files
encrypt.py
contains the encryption code and
data.txt
with
n, e, c. So let’s look at the script.
from Crypto.Util import number
import gmpy
m = open("flag.txt").read().replace("\n","")
phi = open("phi.txt").read().replace("\n","")
n = 7337791914468017448993421081682268029926821634187929635993608507353753574551499799637986960151611974754140244680333893009516941301449968186658243713185925313371652987596878243169447204564056755051626555035757949473740058691726154896381102726587...
e = 65537
d = str(gmpy.invert(e,long(phi)))
c = ""
count = 0
for i in m:
c += chr(ord(i) ^ ord(d[count]))
count +=1
count = count % len(d)
f = open("data.txt","w")
f.write("n = "+str(n)+"\n")
f.write("e = "+str(e)+"\n")
f.write("c = "+str(int(c.encode("hex") ,16)))
f.close()Analyzing the Script
The script reads the flag and the
Euler Totient
from the files, then it computes the
private key
d and
converts the value into a string format. After that, it performs
bitwise
xor
for every character of the flag with the current digit value of
private key. And if the length of the flag
exceeds the length of the
d, it
starts from the beginning.
So, our goal here is to find the
phi
the Euler Totient, so first I always check if
the modulus is weak so we can factor it and get the
totient. Let’s start with
Sage to see if it’s able to find it.
sage: n = 7337791914468017448993421081682268029926821634187929635993608507353753574551499799637986960151611974754140244680333893009516941301449968186658243713185925313371652987596878243169447204564056755051626555035757949473740058691726154896381102726587...
sage: euler_phi(n)
73377909905189126231331550652684365590645396669726908290440092265830312112533463538715937884670073678592094918793680845333388031683102981406974547342448279952318202382242220964187073083250901886794429176376704299964212989712011050152775492474201718....
And after a second, I got the Totient. Now,
let’s calculate our private key
d and
perform the same process of the encryption since it was an
xor.
#!/usr/bin/env python3
from Crypto.Util.number import long_to_bytes, inverse
from string import printable
n = 733779191446801744899342108168226802992682163418792963599360850735375357455149979963798696015161197475414024468033389300951694130144996818665824371318592531337165298759687824316944720456405675505162655503575794947374005869172615489638110272658753196202920853560741805676845416811037858748952036992904987436436305070974548294634539634801990942494632039639997750615092947743413718521647333154278856325718278411799389746268450832747014683725257304667674508399893700585665857805431255846507842167088538394622439932419732551109371563524462274634618135383588224491819316026576502189587830733272736383804826745750346676275381694162218907532199742744234494583745211574842002723757725331355540304942746757973848238312752019843407574782457030601680230342220205032750800522763368978779642050636007667833604220218253864829008534150019797632511068212565709143837742993793579734266511459683596315626111107
e = 65537
phi = 733779099051891262313315506526843655906453966697269082904400922658303121125334635387159378846700736785920949187936808453333880316831029814069745473424482799523182023822422209641870730832509018867944291763767042999642129897120110501527754924742017181472014134922352436898847648999114141296756011639240797839415959375186429567732523255866384911985691057682304784789954825628350089759449220126933493040317629211064408059399460407601405491682855575438013770401765389011948710582942997391678583057799447232854359740183897797166883129522924850096072655328522840457562091460328107312851814081641907004144209211783957695980889333745405002859583055670793090375714357793856233403919410782602868239902544818586476052500170009630475120591368655862098745733457668318575129680021842143302161548368533182192522853701935622293350675024090746943812794717632874237390317514915840000000000000000000000000000000
c = 3761829741272145283141558702847898018685351301385367354966819695378446980283150871815816812877
d = str(inverse(e, phi))
enc = long_to_bytes(c).decode()
flag = ""
count = 0
for i in range(len(enc)):
for c in printable:
dig = chr(ord(c) ^ ord(d[count]))
if dig == enc[i]:
flag += c
count += 1 %len(d)
break
print(flag)
And here’s the flag:
ASCWG{RSA_W1TH_X0R_M@Y_B3_S3CURE_?_!_!}
4. Robin Hood (600 points)
This one is harder than the above, this time we were given
3
files
Robin.py
the encryption script,
public.txt
contains the public modulus and
flag.enc
that contains the encrypted flag. Let’s look at the script to
see this time what is it.
from Crypto.Util.number import isPrime
from random import getrandbits
import gmpy
def Generate_Key(k):
...
private,public = Generate_Key(512)
flag = open('flag.txt').read().strip()
c = ""
key = str(private[0])
count = 0
for char in flag:
c+= chr(ord(char) ^ int(key[count]))
count += 1
count = count % len(key)
with open('flag.enc','w') as f:
f.write(str(c.encode("hex")))
with open('public.txt','w') as f:
f.write(str(public))
with open('private.txt','w') as f:
f.write('Private Key = ' + str(private))Analyzing Generate_Key
The script contains
Generate_Key
function that takes one argument, and calculates some
p, q
the primes for our modulus. And performs the same operation as
the previous challenge, but this time with the first computed
prime
p. So,
let’s look at the function and see how it computes the primes.
def Generate_Key(k):
while True:
r=getrandbits(k)
while(r%2):
r=getrandbits(k)
vp = 36655
vq = 6695
c = 5
p = vp + (c*2)*r + (c*3) * r**2
q = vq + (c*17) * r**2 + (c*18) * r
p /= 5
q /= 5
n = p * q
if(isPrime(p) and isPrime(q)):
return [p,q], n
It takes one parameter
k (the
number of bits), and generate an odd random number of bit length
k,
then it computes
p and
q with
some equations and predefined constants
vp, vq, c. Honestly, I was stuck a bit at this one and confused about
what I should do next. So, after a while, I grabbed my
pen and paper, then start writing down the
equations.
Note: Usually, in any competitions, you have to start using a pen and a paper to figure out how things work and see the whole picture of the problem since our brain is always stuck when things get more complicated especially with math.
Solution
Thereafter, I start realizing there was a quadratic equation of
the second degree for each of
p and
q with
3
unknown variables. And I figure it out, if we multiply both
equations, we should get another equation of the fourth degree
with one unknown variable. So, I opened
Sage and put the equations down to start
solving them.
sage: vp = 36655
sage: vq = 6695
sage: c = 5
sage: n = 113948668321218058524178608776158308937314990524880479474723508653712013716271901647034766919176487524382191287095205452401092977813813687685724437490741778959092419268284962551833575757569033748310450519151445011590095099483698787691340256698979179295851803618926557026349520763872559259872490521439782286287743705495962916146351728273076323504001035116456672986538223911662806020760230282909362013751077903410381234858968042812442475265417492653343870126738695387751546493768698211543924269039265650127984404851333970762580775800738196908901853669874661434010127585260870882676079978934113618971909387904969
sage: r = var('r')
sage: p = vp + (c*2)*r + (c*3) * r^2
sage: q = vq + (c*17) * r^2 + (c*18) * r
sage: p /= 5
sage: q /= 5
sage: eq = (p*q == n)
sage: eq.solve(r)[-1]
r == 38662040327839640789764449160087209987841624029005922365997133658480844611997455251013458743464619148794629079719640111081011702703647931902271878973438
The last equation has only
4 real
roots and one of them is the actual
r, the
random number that had produced the primes. Now, let’s calculate
the desired
p
value and do the same process as before.
r = 38662040327839640789764449160087209987841624029005922365997133658480844611997455251013458743464619148794629079719640111081011702703647931902271878973438
p = (vp + (c*2)*r + (c*3) * r**2) // 5
key = str(p)
flag = ''
count = 0
enc = bytes.fromhex(cipher).decode()
for i in range(len(enc)):
for c in printable:
dig = chr(ord(c) ^ int(key[count]))
if dig == enc[i]:
flag += c
count += 1 % len(key)
break
print(flag)
An it prints out the flag:
ASCWG{R@bin_Crypt@_system_1s_N@T_S3cure_Y@u_C@n_S0lve_1t_By_sympy_Thanks_M@th_:)!!}
Note: There’s an alternative solution by using sympy library in python to do the same calculation, but I prefer using Sage, since it has a lot of mathematical features.
5. Simple RSA (900 points)
The challenge was a brain teaser in the beginning, given one
file
rsa.py
contains both the encryption technique and the output. Let’s
look and see what is hidden in that file.
from Crypto.Util.number import *
from flag import flag
def adlit(x):
l = len(bin(x)[2:])
return (2 ** l - 1) ^ x
def genadlit(nbit):
while True:
p = getPrime(nbit)
q = adlit(p) + 31337
if isPrime(q):
return p, q
p, q = genadlit(1024)
n = p * q
e = 65537
c = pow(bytes_to_long(flag), e, n)
print 'n =', n
print 'c =', cAnalyzing The Functions
There are
2
functions
adlit
and
genadlit, and the script generates the actual prime
p
totally random and
q
based on the first function and the other prime. After playing
arround with the
adlit
function, the term
(2 ** l - 1)
is called
Mersenne Numbers
and also a way to produce a number with all its bits are
1.
So, the
adlit
function just flips all the bits of
x, and
this means
x + adlit(x)
is a constant depending on the bit length of
x.
Let’s assume
len(x) = 10, then
x + adlit(x) = 2**10 - 1.
Solution
And from
genadlit
we know that
q = adlit(p) + 31337. Let’s add these two function together
p + q = 2**1024 + 31336, then multiply it with
p and
that produces an equation
p*p - (2**1024 + 31336)*p + n = 0
of one unkown variable
p.
sage: n = 1086059347151205661920262241256144025139770683771043555916206914349777306575603089167657887713630284106624705581830703190813291645828694385836639023490052635544782274382972812769588548274230224112192918598626099759509463483076563136041968...
sage: p = var('p')
sage: C = 2^1024 + 31336
sage: eq = p^2 - C*p + n == 0
sage: eq.solve(p)
[p == 173509964937923341717466377187987711731443073590832335831120897724376654994319963073580348194964561150732030511607397179636304101426618832117604267641009585304242277354586439406620043079223439859441084817377926949737594721576981813864597832780735271879170545255381853787381616680099298297337021537090228401533, p == 6259348548308249055464141890914761630354624303398321442309183433356020811181000059128129127442974870388083368263996178022485667387797790375243162998464539073525616070279045869682176522022654260011998134707078819100555960765481067609315277760091965284179965429204444452565629258380418007498334792533995767019]
Surprisingly, the two roots is the actual values of both
p and
q,
thus we can calculate the private key and solve the challenge.
#!/usr/bin/env python3
from Crypto.Util.number import long_to_bytes, inverse
n = 1086059347151205661920262241256144025139770683771043555916206914349777306575603089167657887713630284106624705581830703190813291645828694385836639023490052635544782274382972812769588548274230224112192918598626099759509463483076563136041968846580629531580905666944235874028659733112057631714810676584999816474519696501541048628329230672526977221684046155650422983499937158627532763528856805275170571070094702062067688025025216737231720875504633123721284044190986360731336688904940717033856849257163570799017987652265974767603676062600800868270071582778716792818528934917029554280846049155522401284858908822512650440127
p = 173509964937923341717466377187987711731443073590832335831120897724376654994319963073580348194964561150732030511607397179636304101426618832117604267641009585304242277354586439406620043079223439859441084817377926949737594721576981813864597832780735271879170545255381853787381616680099298297337021537090228401533
q = 6259348548308249055464141890914761630354624303398321442309183433356020811181000059128129127442974870388083368263996178022485667387797790375243162998464539073525616070279045869682176522022654260011998134707078819100555960765481067609315277760091965284179965429204444452565629258380418007498334792533995767019
c = 927781172721356996305449766363001284108493370112455773799720131754358386407312891568556372958203716250994379542388740141020015394045514733390812290168850035263199388941267607070256574343253907148705878726609193874242901219187946656673254514384498124378465623687573548303654044036378599747407310217562238758341525889610008694064298579304437255525585375869805936360771337668605391903643701309651970287841207677841155646038534446626286729509041743868962083535803167802791931636828574173570878789903115905853360233358440912012562807628345043544450909430784331831609847563581621013672624989596330971594682912505838157055
e = 65537
phi = (p - 1)*(q - 1)
d = inverse(e, phi)
print(long_to_bytes(pow(c,d,n)))
And here’s the flag:
ASCWg{1t_1s_Equ_0f_2nd_dgree_n0t_rsa}
6. RSA in Hill (900 points)
This was the last crypto challenge in the compitetion and from
its name looks the most hardest one. We were given a file
challenge.txt
contains
n, e, c
and a link to website that looks like.
So, The server can decrypt any cipher data except the original
one
c and
prints out
This Encrypted Data is BlackListed. After a lot of time thinking about it, I recognized this is
chosen ciphertext attack.
Fake Flag
We know from the associative property of the
RSA
. If we choose an
X ** e
and multiply with the cipher
c like
image below, we can submit the value to the server, and the
result would be
MX
where
M is
the flag.
Let’s apply that in the decryption process of RSA and replacing the cipher with the modified one. By that, we tricked the server and it won’t able to recognize the ciphertext, but the result is a known to us.
#!/usr/bin/env python3
n = 20580335879837436674859071914661102533603763859644324111467207592933513867951407018920184140413335593495688620355264082179184998877838393173589733049874351925647637358787208286532265092393801006817663025106117921963950745777612191751854137579567853336804399439686832208046020113050515714602696888849594149396050014316432786882492725374980736730745197387623367211303437605621006718383352476521639568191562811544955606182881838037539517709033544492808023579527471416276713947542826539502246781768733294960018058794205257270476705658408679301457971671378901116100315060343231402422113197146973850048060004297910380994083
c = 16733096479726038887064613814365139185675747243798510559561013942658490133732357653998290998851006278642434288252716299072287150027581029785252826351479077149537004553055504177252888721692623709436535878145267512199622644335552115156335943738812037841121571834398511220512858084649588039086409397130469183632110088444549868739241123838313242124363171915461435619879596621102388201349544842926387866443600766182648509136921374615040566431946374252889753784353143017279303157926697768154694353716934067458953288277560148139403114824280887021201598055808518526048927949669381500648048020335641479490868444242081791377348
e = 65537
modified = c * pow(2,e,n) % n
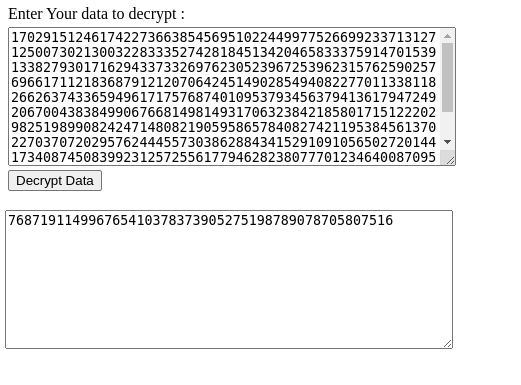
modified = 170291512461742273663854569510224499775266992337131271250073021300322833352742818451342046583337591470153913382793017162943373326976230523967253962315762590257696617112183687912120706424514902854940822770113381182662637433659496171757687401095379345637941361794724920670043838499067668149814931706323842185801715122202982519899082424714808219059586578408274211953845613702270370720295762444557303862884341529109105650272014417340874508399231257255617794628238077701234640087095670231702377891620426172248004658192487595500696995485066683551916743419800722767414501286740296412815866042489257310327168844074949594403
After submitting the value to the server, the result was
768719114996765410378373905275198789078705807516, but this is not the actual flag we should divide that by our
number, I chose
2 in
my case.
Analyzing Hill Cipher
Now, I convert the value to bytes and I got
CSGUOLGIOMXBSFIHODPN
and it was all non-sense words. But from the name of the
challenge
RSA in Hill, maybe it has something with
Hill Cipher, I realized that the output has a length of
20 all
uppercase. So the key must be of length
4,
since
2x2
key matrix, and it is feasible to brute-force the key values
with
26**4 = 456976
possible keys.
Note: The following part I used my little experience with numpy library in python in order to perform the matrix operations easily. You can do your own work after analyzing the cipher.
Getting the Keys
We can perform known plaintext attack on the
first
4
bytes of the flag
ASCW
to get all the possible keys. After converting those bytes into
2x2
integer matrix, then apply matrix multiplication with a key. if
it is equal to the first
4
bytes of the fake flag
CSGU,
append the key matrix with modular inverse of
26 to
our possible keys.
#!/usr/bin/env python3
from string import ascii_uppercase as letters
from Crypto.Util.number import long_to_bytes
from itertools import product
import numpy as np
def mod_inv(mat, mod):
det = np.linalg.det(mat)
return inverse(det,mod)*np.array([[mat[1,1], -mat[0,1]],[-mat[1,0], mat[0,0]]])%mod
def to_num(arr):
return list(map(lambda x: ord(x) - ord('A'), arr))
m = 768719114996765410378373905275198789078705807516 // 2
flag_hill = long_to_bytes(m).decode()
known_plain = np.array(to_num('ASCW')).reshape(2,2)
all_keys = []
for k in product(letters,letters,letters,letters):
key = np.array(to_num(k)).reshape(2,2)
mult = ''.join([letters[i] for i in known_plain.dot(key).reshape(4)%26])
if mult == flag_hill[:4]:
try:
all_keys.append(np.array(mod_inv(key,26)))
except:
passGetting the Flag
Eventually, we got all the possible keys, let’s try them and
search for the known part
ASCWG
in all the possible decrypted flags.
for key in all_keys:
flag = ''
for i in range(0,len(flag_hill),4):
enc = np.array(to_num(flag_hill[i:i+4])).reshape(2,2)
flag += ''.join([letters[i] for i in enc.dot(key).reshape(4)%26])
if 'ASCWG' in flag:
print(flag)
break
The flag:
ASCWG{RSAWITHKPAHILLL}
Conclusion
In the end, all the challenges were RSA with
different attacks and techniques
chosen ciphertext,
known plaintext, and
message signing attacks. During the 8 hours
competition, the coolest thing was playing around with some math
and equations trying to solve them and getting the flags. I’d
like to send my regards to all of my teammates for helping me
out and to the organizers for nudging us during the competition.
If you need any help understanding any of the explanations above
DM
me.